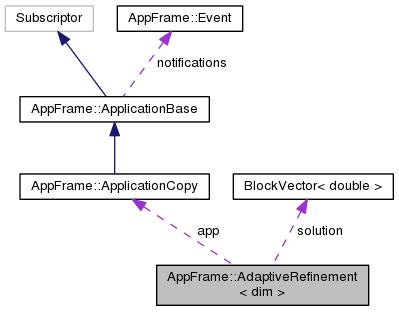
This class is initialized with an application that describes the linearization of the problem that we would like to solve and the nonlinear solved that drives the process (usually a Newton loop). More...

#include <adaptive_refinement.h>

Collaboration diagram for AppFrame::AdaptiveRefinement< dim >:

[legend]

Public Member Functions
	AdaptiveRefinement (AppFrame::OptimizationBlockMatrixApplication< dim > &app_lin, AppFrame::ApplicationCopy &app, const AppFrame::FEVector &solution=AppFrame::FEVector())
	Constructor.

	~AdaptiveRefinement ()

void	declare_parameters (ParameterHandler &param) const
	Declare all parameters that are needed for:

void	set_parameters (const std::vector< std::string > &name_dvar, const std::vector< double > &value_dvar, ParameterHandler &param)
	Reset the parameters used to compute the linear solver equations.

void	initialize (ParameterHandler &param)
	Set up how many equations are needed and read in parameters for the parameter handler in order to initialize data.

void	solve (const std::string param_file, ParameterHandler &param)
	Solve the nonlinear problem.

void	test_derivatives (const std::string input_file, const std::string dvar, const double value, std::vector< double > &resp, std::vector< std::vector< double > > &dresp, const bool gradient=true)
	Member function used to test the derivatives.

void	print_parameters () const
	Print parameters:

void	run_Newton ()
	Run Newton application.

void	run_Newton (std::vector< double > &resp)
	Run Newton application.

void	run_Newton (std::vector< double > &resp, std::vector< std::vector< double > > &dresp_dl)
	Run Newton application.

const AppFrame::FEVector &	get_solution () const
	This function returns `solution`.

Private Attributes
bool	output_initial_mesh
	Flag to output the initial grid to be solved.

bool	output_initial_sol
	Flag to output the initial grid to be solved.

std::string	filename_initial_mesh
	Filename where to output the initial grid.

std::string	filename_initial_sol
	Filename where to output the initial grid.

bool	output_intermediate_sol

bool	output_final_sol

bool	output_intermediate_resp

bool	output_coarse_solution

bool	read_in_initial_solution

unsigned int	n_ref
	Number of initial refinements for the original mesh.

bool	gradients
	Compute the gradients?

AppFrame::OptimizationBlockMatrixApplication < dim > *	app_linear
	Pointer to application.

AppFrame::ApplicationCopy *	app
	Poiner to nonlinear application.

AppFrame::FEVector	solution
	Global FE solution at the support points of the computational domain.

Detailed Description

template<int dim>
class AppFrame::AdaptiveRefinement< dim >

This class is initialized with an application that describes the linearization of the problem that we would like to solve and the nonlinear solved that drives the process (usually a Newton loop).

Then, this class implements the adaptive refinement loop for the application.

This class needs two inputs:

Refinement levels
Analytical gradients

Author: M. Secanell, 2006-13

Constructor & Destructor Documentation

template<int dim>

AppFrame::AdaptiveRefinement< dim >::AdaptiveRefinement	(	AppFrame::OptimizationBlockMatrixApplication< dim > &	app_lin,
		AppFrame::ApplicationCopy &	app,
		const AppFrame::FEVector &	solution = `AppFrame::FEVector()`
	)

Constructor.

template<int dim>

AppFrame::AdaptiveRefinement< dim >::~AdaptiveRefinement ( )

Member Function Documentation

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::declare_parameters ( ParameterHandler & param ) const

Declare all parameters that are needed for:

control of adaptive refinement loop
control of output options during the loop, e.g. return the solution at each cycle

Currently the options implemented are:

subsection Adaptive refinement
  set Number of Refinements = 1                   # Number of adaptive refinements used
  set Output initial mesh = false                 # Set flag to true if you want to output a EPS figure of the initial mesh using the value in file initial mesh
  set Output initial mesh filename = initial_mesh # File where the initial mesh will be output
  set Output initial solution = false             # Set flag to true if you want to output the initial solution to file
  set Initial solution filename = initial_sol     # File where the initial solution will be output
  set Output intermediate solutions = true        # Output the solution after each adaptive refinement level
  set Output intermediate responses = true        # Output any functional such as current density at each refinement level
  set Output final solution = true                # Output final solution to a file named fuel_cell-sol-cycleX where X is the cycle name.
  set Output solution for transfer = false        # Check whether a solution on a refined grid should be output to file on a coarse mesh
  set Read in initial solution from file = false  # Check whether a stored solution should be read from file and applied to the grid
end

template<int dim>

const AppFrame::FEVector& AppFrame::AdaptiveRefinement< dim >::get_solution ( ) const

inline

This function returns solution.

References AppFrame::AdaptiveRefinement< dim >::solution.

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::initialize ( ParameterHandler & param )

Set up how many equations are needed and read in parameters for the parameter handler in order to initialize data.

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::print_parameters ( ) const

Print parameters:

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::run_Newton ( )

Run Newton application.

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::run_Newton ( std::vector< double > & resp )

Run Newton application.

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::run_Newton	(	std::vector< double > &	resp,
		std::vector< std::vector< double > > &	dresp_dl
	)

Run Newton application.

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::set_parameters	(	const std::vector< std::string > &	name_dvar,
		const std::vector< double > &	value_dvar,
		ParameterHandler &	param
	)

Reset the parameters used to compute the linear solver equations.

Note: Mainly used for optimization

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::solve	(	const std::string	param_file,
		ParameterHandler &	param
	)

Solve the nonlinear problem.

template<int dim>

void AppFrame::AdaptiveRefinement< dim >::test_derivatives	(	const std::string	input_file,
		const std::string	dvar,
		const double	value,
		std::vector< double > &	resp,
		std::vector< std::vector< double > > &	dresp,
		const bool	gradient = `true`
	)